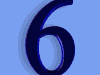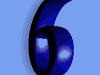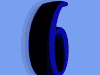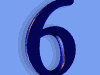
Animated Logo

公式 2

目次

全称記号

存在記号

述語論理

公式1

公式2

公式3

式の簡単化1

式の簡単化2

TEST

全称記号は and と親戚なので
    4.　(∀x)(f(x) and g(x)) = (∀x)(f(x))and (∀x)(g(x))

    = (∀x)(f(x))and (∀y)(g(y))

また同様に
    5.　(∃x)(f(x) or g(x)) = (∃x)(f(x)) or (∃x)(g(x))

    = (∃x)(f(x)) or (∃y)(g(y))

and と or が逆の場合には等号がいえないので注意が必要です．しかし 4.で g(x) が x に無関係な場合には次の式が成り立ちます．　
    6. (∀x)(f(x) or G) = (∀x)(f(x)) or G
同様に
    7. (∃x)(f(x) and G) = (∃x)(f(x)) and G
命題関数が限定作用素中の変数を含まない場合限定作用素を取ることができます．
    8. (∀x)(G) = G 8'. (∀x)(f(y)) = f(y)

    9. (∃x)(G) = G 9'. (∃x)(f(y)) = f(y)

特に
    10. (∀x)(True) = True 10'. (∀x)(False) = False

    11. (∃x)(True) = True 11'. (∃x)(False) = False

      また前にも説明しましたが，束縛変数は他の記号でもよいので
        12. (∀x)(f(x)) = (∀y)(f(y))

        13. (∃x)(f(x)) = (∃y)(f(y))