B.8 FINSEQ_1

FINSEQ_1.ABS (Digest)
Segments of Natural Numbers and Finite Sequences, by Grzegorz Bancerek and Kryzysztof Hryniewiecki

reserve k,l,m,n,k1,k2 for Nat,

   X,Y,Z          for set,

   x,y,z,y1,y2    for Any,

   f,g,h          for Function;



def 1 func Seg n -> set means it = { k : 1  k & k  n };



1 Seg n = { k : 1  k & k  n } ;

3 k C Seg n iff 1  k & k  n;

4 Seg 0  =  & Seg 1 = { 1 } & Seg 2 = { 1,2 };

5 n = 0 or n C Seg n;

6 n+1 C Seg(n+1);

7 n  m iff Seg n c= seg m;

8 Seg n = Seg m implies n = m;

9 k  n implies Seg k = Seg k  Seg n & Seg k = Seg n  Seg k;

10 (Seg k = Seg k  Seg n or Seg k = Seg n  Seg k )

   implies k  n;

11 Seg n U { n+1 } = Seg (n+1);



def 2 attr FinSequence-like -> Function means

      ex n st dom it = Seg n ;



cluster FinSequence-like Function;



mode FinSequence is FinSequence-like Function;



reserve p,q,r,s,t,v for FinSequence;



def 3 func len p -> Nat means Seg it = dom p;



14  is FinSequence;



theorem :: FINSEQ_1:15

   (ex k st dom f c= Seg k) implies

      ex p st f c= p;



scheme SeqEx{A( )->Nat,P[Any,Any]}:

  ex p st dom p = Seg A ( ) & for k st k C Seg A ( ) holds P[k,p.k]

  provided

    for k,y1,y2 st k C Seg A( ) & P[k,y1] & P[k,y2] holds y1=y2

      and for k st k C Seg A( ) ex x st P[k,x];



scheme SeqLambda{A( )->Nat,F(Any) -> Any} :

  ex p being FinSequence st len p = A( )

  & for k st k C Seg A( ) holds p.k=F(k);



16 z C p implies

    ex k st (k C dom p & z=[k,p.k]);

17 X = dom p & X = dom q & (for k st k C X holds p.k = q.k) implies p=q;

18 for p,q st

    (len p = len q) & for k st 1  k & k  len p holds p.k=q.k

    holds p=q;

19 p 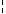 (Seg n) is FinSequence;

20 (rng p c= dom f) implies (fp is FinSequence);

21 k  len p & q = p 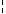(Seg k) implies len q = k & dom q = Seg k;



def 4 mode FinSequence of D -> FinSequence means rng it c= D ;



cluster  -> FinSequence-like;

cluster FinSequence-like PartFunc of NAT,D;



reserve D,D1,D2 for set;



23 for D,k for p being FinSequence of D

     holds p 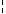 (Seg k) is FinSequence of D;

24 for D being non empty set

     ex p being FinSequence of D st len p = k;



cluster empty FinSequence;



25 len p = 0 iff p = <>;

26 p=<> iff dom p = ;

27 p=<> iff rng p=;

29 for D be set holds <> is FinSequence of D;



cluster empty FinSequence of D;



def 6 func <>(D) iff len p = 0;



32 p=<>(D) iff len p = 0;



def 7 func p^q -> FinSequence means

      dom it = Seg (len p + len q)

       & (for k st k C dom p holds it.k=p.k)

       & (for k st k C dom q holds it.(len p + k) = q.k);



35 len(p^q) = len p + len q;

36 for k st len p + 1  k & k  len p + len q holds (p^q).k = q.(k-len p);

37 len p < k & k  len(p^q) implies (p^q).k = q.(k - len p);

38 k C dom (p^q)

  implies (kC dom p or (ex n st n C dom q & k=len p + n));

39 dom p c= dom(p^q);

40 x C dom q implies ex k st k=x & len p + k C dom(p^q);

41 k C dom q implies len p + k C dom(p^q);

42 rng p c= rng(p^q);

43 rng q c= rng(p^q);

44 rng(p^q) = rng p U rng q;

45 p^q^r = p^(q^r);

46 p^r = q^r or r^p = r^q implies p = q;

47 p^<>= p & <>^p = p;

48 p^q =<> implies p=<> & q=<>;



def 8  func <*x*> -> FinSequence means dom it = Seg 1 & it.1 = x;



50 p^q is FinSequence of D

    implies p is FinSequence of D & q is FinSequence of D;



def 9 func <*x,y*> -> FinSequence means it = <*x*>^<*y*> ;

def 10 func <*x,y,z*> -> FinSequence menas

        it = <*x*>^<*y*>^<*z*>;



52 <*x*> = { [1,x] };

53 <*x,y*> = <*x*>^<*y*>;

54<*x,y,z*> = <*x*>^<*y*>^<*z*>;

55 p=<*x*> iff dom p = Seg 1 & rng p = {x};

56 p=<*x*> iff len p = 1 & rng p = {x};

57 p = <*x*> iff len p = 1 & p.1 = x;

58 (<*x*>^p).1 = x;

59 (p^<*x*>).(len p + 1)=x;

60 <*x,y,z*>=<*x*>^<*y,z*> & <*x,y,z*>=<*x,y*>^<*z*>;

61 p = <*x,y*> iff len p = 2 & p.1=x & p.2=y;

62 p = <*x,y,z*> iff len p = 3 & p.1 = x & p.2 = y & p.3 = z;

63 for p st p < > <> holds ex q,x st p=q^<*x*>;
                          


scheme IndSeq{P[FinSequence]}:

   for p holds P[p]

   provided

   P[<>] and

   for p,x st P[p] holds P[p^<*x*>];



64 for p,q,r,s being FinSequence st p^q = r^s & len p  len r

     ex t being FinSequence st p^t = r;



def 11 func D* -> non empty set means

    x C it iff x is FinSequence of D ;



65 x C D* iff x is FinSequence of D;

66 <> C D*;



scheme SepSeq{D( )->non empty set, P[FinSequence]} :

   ex X st (for x holds x C X iff

     ex p st (p C D( )* & P[p] & x=p));



def 12 attr FinSubsequence-like -> Function means

        ex k st dom it c= Seg k;



cluster FinSubsequence-like Function;



mode FinSubsequence is FinSubsequence-like Function;



68 for p being FinSequence holds p is FinSubsequence;

69 for p,X holds (p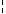X is FinSubsequence & Xp is FinSubsequence);



reserve p',q' for FinSubsequence;



def 13 func Sgm X -> FinSequence of NAT means

         rng it = X & for l,m,k1,k2 st ( 11 & 1 < m & m  len it 

         & k1=it.1 & k2=it.m) holds k1 < k2;



71 rng Sgm dom p' = dom p';



def 14 func Seq p' -> FinSequence means it = p'  Sgm(dom p');



72 for X st ex k st X c= Seg k holds Sgm X = <> iff X = ;