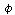 E -> empty Subset of E means it =
E -> empty Subset of E means it = 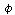 ;
;def 2 func
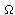 E ->manes it = E;
E ->manes it = E;SUBSET_1.ABS (Digest)
Properties of Subsets, by Zinaida Trybulec.
reserve E,X for set;
reserve x,y for Any;
cluster empty Subset of E;
def 1 func 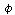 E -> empty Subset of E means it =
E -> empty Subset of E means it = 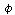 ;
;
def 2 func 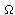 E ->manes it = E;
E ->manes it = E;
4 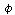 is Subset of X;
is Subset of X;
reserve A,B,C for Subset of E;
7 (for x being Element of E holds x C A implies x CB) implies A c= B;
8 (for x being Element of E holds x C A iff x C B) implies A = B;
def 3 func A-> Subset of E means it = E
A; func A U B -> Subset of E; func A
B -> Subset of E; func A
B -> Subset of E; func A
B -> Subset of E;
15 (for x being Element of E holds x
CA iff xCB or xCC) implies A = B U C; 16 (for x being Element of E holds xCA iff xCB & xCC) implies A = BC; 17 (for x being Element of E holds x
CA iff xCB & not xCC) implies A = BC; 18 (for x being Element of E holds x
CA iff not(xCB iff xCC)) implies A = BC; 20
E = E; 21
E = (
E)
; 22
E = (
E)
; 23 A
= E
A; 24 A
= A; 25 A U A
=
E & A
U A =
E; 26 A
A
=
E & A

A =
E; 28 A U
E =
E &
E U A =
E; 29 (A U B)
= A

B
30 (A
B)
= A
U B
; 31 A c= B iff B
c= A
; 32 A
B = A
B
; 33 (A
B)
= A
U B; 34 (A
B)
= A
B U A

B
; 35 A c= B
implies B c= A
; 36 A
c= B implies B
c= A; 38 A c= A
iff A =
E; 39 A
c= A iff A =
E; 40 X c= A & X c= A
implies X =
; 41 (A U B)
c= A
& (A U B)
c= B
; 42 A
c= (A
B)
& B
c= (A
B)
; 43 A misses B iff A c= B
; 44 A misses B
iff A c= B; 45 A misses A
; 46 A misses B & A
misses B
implies A = B
; 47 A c= B & C misses B implies A c= C
; 48 (for a being Element of A holds a
CB) implies A c= B; 49 (for x being Element of E holds xCA) implies E = A; 50 E < >implies for A,B holds A = B
iff for x being Element of E holds x
CA iff not xCB; 51 E < >implies for A,B holds A = B
iff for x being Element of E holds not x
CA iff xCB; 52 E < >implies for A,B holds A = B
iff for x being Element of E holds not(x
CA iff xCB); 53 xCAimplies not x
CA;reserve x1,x2,x3,x4,x5,x6,x7,x8 for Element of X;
54 X < >
implies {x1} is Subset of X; 55 X < >
implies {x1,x2} is Subset of X; 56 X < >
implies {x1,x2,x3} is Subset of X; 57 X < >
implies {x1,x2,x3,x4} is Subset of X; 58 X < >
implies {x1,x2,x3,x4,x5} is Subset of X; 59 X < >
implies {x1,x2,x3,x4,x5,x6} is Subset of X; 60 X < >
implies {x1,x2,x3,x4,x5,x6,x7} is Subset of X; 61 X < >
implies {x1,x2,x3,x4,x5,x6,x7,x8} is Subset of X;
reserve x1,x2,x3,x4,x5,x6,x7,x8 for Any;
62 x1
CX implies {x1} is Subset of X;scheme Subset_Ex { A( )-> set,P[Any] } : ex X being Subset of A( ) st for x holds x
CX iff xCA( ) & P[x];