Functions from a Set to a Set, by Czes{
 1aw Byli
1aw Byli 'nski.
'nski.FUNCT_2.ABS (Digest)
Functions from a Set to a Set, by Czes{ 1aw Byli
1aw Byli 'nski.
'nski.
reserve P,Q,X,X1,X2,Y,Y1,Y2,Z for set;
reserve p,q,x,x1,x2,y,y1,y2,z,z1,z2 for Any;
def 1 mode Function of X,Y -> Function means
X = dom it & rng it c= Y if Y =  implies X =
implies X =  otherwise it =
otherwise it =  ;
;
2 for f being Function of X,Y
holds ((Y < >  or X =
or X =  ) implies X = dom f) & rng f c= Y;
3 for f being Function holds f is Function of dom f, rng f;
4 for f being Fucntion st rng f c = Y holds f is Function of dom f, Y;
5 for f being Function st dom f = X & for x st x
) implies X = dom f) & rng f c= Y;
3 for f being Function holds f is Function of dom f, rng f;
4 for f being Fucntion st rng f c = Y holds f is Function of dom f, Y;
5 for f being Function st dom f = X & for x st x C X holds f.x C Y
holds f is Function of X,Y;
6 for f being Function of X,Y st Y < >  & x
& x C X holds f.x C rng f;
7 for f being Function of X,Y st Y < >  & x
& x C X holds f.x C Y;
8 for f being Function of X,Y st (Y =  implies X =
implies X =  ) & rng f c= Z
holds f is Function of X,Z;
9 for f being Function of X,Y st (Y =
) & rng f c= Z
holds f is Function of X,Z;
9 for f being Function of X,Y st (Y =  implies X =
implies X =  ) & Y c= Z
holds f is Function of X,Z;
) & Y c= Z
holds f is Function of X,Z;
scheme FuncEx1{X( )->set,Y( )->set,P[Any,Any]}:
ex f being Function of X( ), Y( ) st for x st x C X( ) holds P[x,f.x]
provided
for x st x C X( ) ex y st y C Y( ) & P[x,y] and
for x,y1,y2 st x C X( ) & P[x,y1] & P[x,y2] holds y1 = y2;
scheme Lambda1{X( )->set,Y( )->set,F(Any)->Any}:
ex f being Function of X( ),Y( ) st for x st x C X( ) holds f.x = F(x)
provided
for x st x C X ( ) holds F(x) C Y( );
def 2 func Funcs(X,Y) -> set means x C it
iff ex f being Function st x = f & dom f = X & rng f c= Y;
11 for f being Function of X,Y st Y =  implies X =
implies X =  holds f
holds f C Funcs(X,Y);
12 for f being Function of X,X holds f C Funcs(X,X);
13 for f being Function of  ,X holds f
,X holds f C Funcs( ,X);
14 X < >
,X);
14 X < >  implies Funcs(X,
implies Funcs(X, ) =
) = ;
15 Funcs(X,Y) =
;
15 Funcs(X,Y) =  implies X < >
implies X < >  & Y =
& Y =  ;
16 for f being Function of X,Y st Y < >
;
16 for f being Function of X,Y st Y < >  & for y st y
& for y st y C Y ex x st x C X & y = f.x holds rng f = Y;
17 for f being Function of X,Y st y C Y
& rng f = Y ex x st x C X & f.x = y;
18 for f1,f2 being Function of X,Y st Y < >  & for x st x
& for x st x C X holds f1.x = f2.x
holds f1 = f2;
19 for f being Function of X,Y for g being Function of Y,Z
st Y =  implies Z =
implies Z =  or X =
or X =  holds g
holds g  f is Function of X,Z;
20 for f being Function of X,Y for being Function of Y,Z
st Y < >
f is Function of X,Z;
20 for f being Function of X,Y for being Function of Y,Z
st Y < >  & Z < >
& Z < >  & rng f = Y & rng g = Z holds rng(g
& rng f = Y & rng g = Z holds rng(g f) = Z;
21 for f being Function of X,Y, g being Function
st Y < >
f) = Z;
21 for f being Function of X,Y, g being Function
st Y < >  & x
& x C X holds (g  f).x = g.(f.x);
22 for f being Function of X,Y st Y < >
f).x = g.(f.x);
22 for f being Function of X,Y st Y < >  holds rng f = Y
iff for Z st Z < >
holds rng f = Y
iff for Z st Z < >  for g,h being Function of Y,Z
st g
for g,h being Function of Y,Z
st g f = h
f = h f holds g = h;
23 for f being Function of X,Y
st Y =
f holds g = h;
23 for f being Function of X,Y
st Y =  implies X =
implies X =  holds f
holds f (id X) = f & (id Y)
(id X) = f & (id Y) f = f;
24 for f being Function of X,Y for g being Function of Y,X
st Y < >
f = f;
24 for f being Function of X,Y for g being Function of Y,X
st Y < >  & f
& f g = id Y holds rng f = Y;
25 for f being Function of X,Y st Y =
g = id Y holds rng f = Y;
25 for f being Function of X,Y st Y =  implies X =
implies X =  holds f is one-to-one
iff for x1,x2 st x1
holds f is one-to-one
iff for x1,x2 st x1 C X & x2 C X & f.x1 = f.x2 holds x1 = x2;
26 for f being Function of X,Y for g being Function of Y,Z
st (Z =  implies Y =
implies Y =  ) & (Y =
) & (Y =  implies X =
implies X =  )
& g
)
& g f is one-to-one holds f is one-to-one;
27 for f being Function of X,Y st X < >
f is one-to-one holds f is one-to-one;
27 for f being Function of X,Y st X < >  & Y < >
& Y < >  holds f is one-to-one
iff for Z for g,h being Function of Z,X st f
holds f is one-to-one
iff for Z for g,h being Function of Z,X st f g = f
g = f h holds g = h;
28 for f being Function of X,Y for g being Function of Y,Z
st Z < >
h holds g = h;
28 for f being Function of X,Y for g being Function of Y,Z
st Z < >  & Y < >
& Y < >  & rng(g
& rng(g f) = Z & g is one-to-one holds rng f = Y;
29 for f being Function of X,Y for g being Function of Y,X
st X < >
f) = Z & g is one-to-one holds rng f = Y;
29 for f being Function of X,Y for g being Function of Y,X
st X < >  & Y < >
& Y < >  & g
& g f = id X holds f is one-to-one & rng g = X;
30 for f being Function of X,Y for g being Function of Y,Z
st (Z =
f = id X holds f is one-to-one & rng g = X;
30 for f being Function of X,Y for g being Function of Y,Z
st (Z =  implies Y =
implies Y =  ) & g
) & g f is one-to-one & rng f = Y
holds f is one-to-one & g is one-to-one;
31 for f being Function of X,Y
st f is one-to-one & (X =
f is one-to-one & rng f = Y
holds f is one-to-one & g is one-to-one;
31 for f being Function of X,Y
st f is one-to-one & (X =  iff Y =
iff Y =  ) & rng f = Y
holds f" is Function of Y,X;
32 for f being Function of X,Y
st Y < >
) & rng f = Y
holds f" is Function of Y,X;
32 for f being Function of X,Y
st Y < >  & f is one-to-one & x
& f is one-to-one & x C X holds (f").(f.x) = x;
34 for f being Function of X,Y for g being Function of Y,X
st X < >  & Y < >
& Y < >  & rng f = Y & f is one-to-one
& for y,x holds y
& rng f = Y & f is one-to-one
& for y,x holds y C Y & g.y = x iff x C X & f.x = y
holds g = f";
35 for f being Function of X,Y st Y < >  & rng f = Y
& f is one-to-one holds f"
& rng f = Y
& f is one-to-one holds f" f = id X & f
f = id X & f f" = id Y;
36 for f being Function of X,Y for g being Function of Y,X
st X < >
f" = id Y;
36 for f being Function of X,Y for g being Function of Y,X
st X < >  & Y < >
& Y < >  & rng f = Y & g
& rng f = Y & g f = id X
& f is one-to-one
holds g = f";
37 for f being Function of X,Y
st Y < >
f = id X
& f is one-to-one
holds g = f";
37 for f being Function of X,Y
st Y < >  & ex g being Function of Y,X st g
& ex g being Function of Y,X st g f = id X
holds f is one-to-one;
38 for f being Function of X,Y
st(Y =
f = id X
holds f is one-to-one;
38 for f being Function of X,Y
st(Y =  implies X =
implies X =  ) & Z c= X holds f
) & Z c= X holds f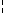 Z is Function of Z,Y;
39 for f being Function of X,Y st Y < >
Z is Function of Z,Y;
39 for f being Function of X,Y st Y < >  & x
& x C X & x C Z
holds (f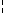 Z).x = f.x;
40 for f being Function of X,Y st X c= Z holds f
Z).x = f.x;
40 for f being Function of X,Y st X c= Z holds f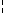 Z = f;
41 for f being Function of X,Y st Y < >
Z = f;
41 for f being Function of X,Y st Y < >  & x
& x C X & f.x C Z
holds (Z f).x = f.x;
42 for f being Function of X,Y st (Y=
f).x = f.x;
42 for f being Function of X,Y st (Y=  implies X =
implies X =  )
& Y c= Z holds Z
)
& Y c= Z holds Z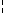 f = f;
43 for f being Function of X,Y st Y < >
f = f;
43 for f being Function of X,Y st Y < >  for y holds y
for y holds y C f P iff ex x st x
P iff ex x st x C X & x C P & y = f.x;
44 for f being Function of X,Y st Y =  implies X =
implies X =  holds f
holds f X = rng f;
45 for f being Function of X,Y st Y =
X = rng f;
45 for f being Function of X,Y st Y =  implies X =
implies X =  holds f
holds f X = rng f;
46 for f being Function of X,Y
st Y < >
X = rng f;
46 for f being Function of X,Y
st Y < >  for x holds x
for x holds x C f"Q iff xCX & f.x C Q;
47 for f being Function of X,Y st Y =  implies X =
implies X =  holds f"Q c= X;
48 for f being Function of X,Y st Y =
holds f"Q c= X;
48 for f being Function of X,Y st Y =  implies X =
implies X =  holds f"Y = X;
49 for f being Function of X,Y
st Y < >
holds f"Y = X;
49 for f being Function of X,Y
st Y < >  holds (for y st y
holds (for y st y C Y holds f"{y} < >  ) iff rng f = Y;
50 for f being Function of X,Y
st (Y =
) iff rng f = Y;
50 for f being Function of X,Y
st (Y =  implies X =
implies X =  ) & P c= X holds P c= f"(f
) & P c= X holds P c= f"(f P);
51 forf being Function of X,Y st Y =
P);
51 forf being Function of X,Y st Y =  implies X =
implies X =  holds f"(f
holds f"(f X) = X;
53 for f being Function of X,Y for g being Function of Y,Z
st (Z =
X) = X;
53 for f being Function of X,Y for g being Function of Y,Z
st (Z =  implies Y =
implies Y =  ) & (Y =
) & (Y =  implies X =
implies X =  )
holds f"Q c= (f
)
holds f"Q c= (f g)"(g
g)"(g Q);
54 for f being Function of
Q);
54 for f being Function of  ,Y holds dom f =
,Y holds dom f =  & rng f =
& rng f =  ;
55 for f being Function st dom f =
;
55 for f being Function st dom f =  holds f is Function of
holds f is Function of  ,Y;
56 for f1 being Function of
,Y;
56 for f1 being Function of  ,Y1 for f2 being Function of
,Y1 for f2 being Function of  ,Y2
holds f1 = f2;
57 for f being Function of
,Y2
holds f1 = f2;
57 for f being Function of  ,Y for g being Function of Y,Z
holds g
,Y for g being Function of Y,Z
holds g f is Function of
f is Function of  ,Z;
58 for f beinb Function of
,Z;
58 for f beinb Function of  ,Y holds f is one-to-one;
59 for f being Function of
,Y holds f is one-to-one;
59 for f being Function of  ,Y holds f
,Y holds f P =
P =  ;
60 for f being Function of
;
60 for f being Function of  ,Y holds f"Q =
,Y holds f"Q =  ;
61 for f being Function of {x},Y st Y < >
;
61 for f being Function of {x},Y st Y < >  holds f.x
holds f.x C Y;
62 for f being Function of {x},Y st Y < >  holds rng f = {f.x};
63 for f being Function of {x},Y st Y < >
holds rng f = {f.x};
63 for f being Function of {x},Y st Y < >  holds f is one-to-one;
64 for f being Function of {x},Y st Y < >
holds f is one-to-one;
64 for f being Function of {x},Y st Y < >  holds f
holds f P c= {f.x};
65 for f being Function of X,{y} st x
P c= {f.x};
65 for f being Function of X,{y} st x C X holds f.x = y;
66 for f1,f2 being Function of X,{y} holds f1 = f2;
67 for f being Function of X,X holds dom f = X & rng f c= X;
69 for f being Function of X,X st x C X holds f.x C X;
70 for f being Function of X,X, g being Function
st x C X holds (g f).x = g.(f.x);
73 for f,g being Function of X,X st rng f = X & rng g = X
holds rng(g
f).x = g.(f.x);
73 for f,g being Function of X,X st rng f = X & rng g = X
holds rng(g f) = X;
74 for f being Function of X,X holds f
f) = X;
74 for f being Function of X,X holds f (id X) = f & (id X)
(id X) = f & (id X) f = f;
75 for f,g being Function of X,X st g
f = f;
75 for f,g being Function of X,X st g f = f & rng f = X holds g = id X;
76 for f,g being Function of X,X st f
f = f & rng f = X holds g = id X;
76 for f,g being Function of X,X st f g = f & f is one-to-one
holds g = id X;
77 for f being Function of X,X
holds f is one-to-one
iff for x1,x2 st x1
g = f & f is one-to-one
holds g = id X;
77 for f being Function of X,X
holds f is one-to-one
iff for x1,x2 st x1 C X & x2 C X & f.x1 = f.x2 holds x1 = x2;
78 for f being Function of X,X holds f P c= X;
79 for f being Function of X,X holdsf
P c= X;
79 for f being Function of X,X holdsf X = rng f;
80 for f being Function of X,X holds f"Q c= X;
82 for f being Function of X,X holds f"(f
X = rng f;
80 for f being Function of X,X holds f"Q c= X;
82 for f being Function of X,X holds f"(f X) = X;
X) = X;
def 3 attr Permutation-like -> Function of X,X means
it is one-to-one & rng it = X;
cluster Permutation-like Function of X,X;
mode Permutation of X is Permutation-like Function of X,X;
84 for being Permutation of X holds f is one-to-one & rng f = X;
85 for f being Permutation of X
for x1,x2 st x1 C X & x2 C X & f.x1 = f.x2
holds x1 = x2;
86 for f,g being Permutation of X st g f = g holds f = id X;
87 for f,g being Permutation of X st g
f = g holds f = id X;
87 for f,g being Permutation of X st g f = id X holds g = f";
88 for f being Permutation of X holds (f")
f = id X holds g = f";
88 for f being Permutation of X holds (f") f=id X & f
f=id X & f (f") = id X;
89 for f being Permutation of X holds (f")"=f;
90 for f ,g being Permutation of X holds (g
(f") = id X;
89 for f being Permutation of X holds (f")"=f;
90 for f ,g being Permutation of X holds (g f)"=f"
f)"=f" g";
91 for f being Permutation of X st P
g";
91 for f being Permutation of X st P 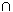 Q =
Q =  holds f
holds f P
P 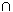 f
f Q =
Q =  ;
92 for f being Permutation of X st P c= X holds f
;
92 for f being Permutation of X st P c= X holds f (f"P) = P & f"(f
(f"P) = P & f"(f P) = P;
93 for f being Permutation of X holds f
P) = P;
93 for f being Permutation of X holds f P = (f")"P & f"P = (f")
P = (f")"P & f"P = (f") P;
P;
reserve C,D,E for non empty set;
def 4 redefine mode Function of X,D means
X=dom it & rng it c= D;
94 for f being Function of X,D holds dom f = X & rng f c= D;
95 for f being Function st dom f = X & rng f c= D
holds f is Function of X,D;
96 for f being Function of X,D st x C X holds f.x C D;
97 for f being Function of {x},D holds f.x C D;
98 for f1,f2 being Function of X,D st for x st x C X holds f1.x = f2.x
holds f1 = f2;
99 for f being Function of X,D for g being Function
st x C X holds (g f).x = g.(f.x);
100 for f being Function of X,D holds f
f).x = g.(f.x);
100 for f being Function of X,D holds f (id X) = f & (id D)
(id X) = f & (id D) f = f;
101 for f being Function of X,D
holds f is one-to-one
iff for x1,x2 st x1
f = f;
101 for f being Function of X,D
holds f is one-to-one
iff for x1,x2 st x1 C X & x2 C X & f.x1 = f.x2 holds x1 = x2;
102 for f being Function of X,D
for y holds y C f P iff ex x st x
P iff ex x st x C X & x C P & y = f.x;
103 for f being Function of X,D holds f P c= D;
104 for f being Function of X,D holds f
P c= D;
104 for f being Function of X,D holds f X = rng f;
106 for f being Function of X,D for x holds x
X = rng f;
106 for f being Function of X,D for x holds x C f"Q iff x C X & f.x C Q;
107 for f being Function of X,D holds f"Q c= X;
108 for f being Function of X,D holds f"D = X;
109 for f being Function of X,D
holds (for y st y C D holds f"{y} < >  ) iff rng f = D;
110 for f being Function of X,D holds f"(f
) iff rng f = D;
110 for f being Function of X,D holds f"(f X) = X;
112 for f being Function of X,D for g being Function of D,E
holds f"Q c= (g
X) = X;
112 for f being Function of X,D for g being Function of D,E
holds f"Q c= (g f)"(g
f)"(g Q);
Q);
reserve c,c1,c2 for Element of C;
reserve d,d1,d2 for Element of D;
scheme FuncExD{C( )->non empty set,D( )->non empty set,P[Any,Any]}:
ex f being Function of C( ),D( ) st for x being Element of C( ) holds P[x,f.x
provided
for x being Element of C( )ex y being Element of D( ) st P[x,y] and
for x being (Element of C( )), y1,y2 being Element of D( )
st P[x,y1] & P[x,y2] holds y1 = y2;
scheme LambdaD{C( )->non empty set,D( )->non empty set,
F((Element of C( )))->Element of D( )}:
ex f being Function of C( ),D( )
st for x being Element of C( ) holds f.x = F(x);
113 for f1,f2 being Function of C,D st for c holds f1.c = f2.c
holds f1 = f2;
116 for f being Function of C,D for d holds d Cf P
iff ex c st c
P
iff ex c st c C P & d = f.c;
118 for f1,f2 being Function of [:X,Y:],Z
st X < >  & for x,y st x
& for x,y st x C X & y C Y holds f1.[x,y] = f2.[x,y]
holds f1 = f2;
119 for f being Function of [:X,Y:],Z st x C X & y C Y & Z < >  holds f.[x,y]
holds f.[x,y] C Z;
scheme FuncEx2{X( )->set,Y( )->set,Z( )->set,P[Any,Any,Any]}:
ex f being Function of [:X( ),Y( ):],Z( ) st
for x,y st x C X( ) & y C Y( ) holds P[x,y,f.[x,y]]
provided
for x,y st x C X( ) & y C Y( ) ex z st z C Z( ) & P[x,y,z] and
for x,y,z1,z2 st x C X( ) & y C Y( ) & P[x,y,z1] & P[x,y,z2]
holds z1 = z2;
scheme Lambda2{X( )->set,Y( )->set,Z( )->set,F(Any,Any)->Any}:
ex f being Function of [:X( ),Y( ):],Z( )
st for x,y st x C X( ) & y C Y( ) holds f.[x,y] = F(x,y)
provided
for x,y st x C X( ) & y C Y( ) holds F(x,y) C Z( );
120 for f1,f2 being Function of [:C,D:],E
st for c,d holds f1.[c,d] = f2.[c,d]
holds f1 = f2;
scheme FuncEx2D{X( )->non empty set,Y( )->non empty set,
Z( )->non empty set,P[Any,Any,Any]}:
ex f being Function of [:X( ),Y( ):],Z( ) st
for x being Element of X( ) for y being Element of Y( )
holds P[x,y,f.[x,y]]
provided
for x being Element of X( ) for y being Element of Y( )
ex z being Element of Z( ) st P[x,y,z] and
for x being Element of X( ) for y being Element of Y( )
for z1,z2 being Element of Z( ) st P[x,y,z1] & P[x,y,z2]
holds z1 = z2;
scheme Lambda2D{X( )->non empty set,Y( )->non empty set,Z( )->non empty set,
F((Element of X( )),Element of Y( ))->Element of Z( )}:
ex f being Function of [:X( ),Y( ):],Z( )
st for x being Element of X( ) for y being Element of Y( )
holds f.[x,y]=F(x,y)