The dictionary of basic mathematical notations in Mizar

 

Mizar Version: 7.0.05

MML Version: 4.09.842

 

C O N T E N T S

 

＜Logical notations＞

＜The notations of set theory＞

＜The notations of the sets of numbers＞

＜The notations for functions (relations)＞

＜The notations of arithmetic＞

＜The notations of numbers and special constants＞

＜The notations of elementary functions and complex numbers＞

＜The notations of limit and series＞

＜The notations of differentiation and integral＞

＜The notations of geometry＞

＜The notations of probability＞

＜The notations of vectors and matrices＞

 

[The way of description for entries in the dictionary]

 

The way of description for entries in the dictionary is, in principle, as follows.

 

＜a usual mathematical notation＞ ＜English explanation of the notation＞ [mizar] ＜its corresponding mizar-notation＞ (＜mizar-article: definition etc. in which the notation occurs＞) [usage] ＜some example using the mizar-notation＞ [＜the explanation of the mizar-example＞]

 

 

 

 

 

 

 

 

＜Logical notations＞

 

1.  ¬（〜，￣ ） negation  [mizar]  not  (build in Mizar system)

 [usage]  not P  [not P]

2.  ∧（&） and  (conjunction)  [mizar]  &  (build in Mizar system)

 [usage]  A & B  [A and B]

3. ∨　or  (disjunction)  [mizar]  or  (build in Mizar system)

 [usage]  A or B  [A or B]

4. →（⇒，⊃）implication  [mizar]  implies  (build in Mizar system)

 [usage]  A implies B  [A implies B]

5. ⇔  equivalence   [mizar]  iff  (build in Mizar system)

 [usage]  A iff B  [A is equivalent to B]

6. ∀ for all   [mizar]  for  (build in Mizar system)

 [usage]  1. for a holds P [for every a, P holds.]

2. for a being set holds P [For every a which is a set, P holds.]

3. for a, b being set holds P [For every a, b which are sets, P holds.]

       4. for a being set st P holds Q [For every set a satisfied with P, Q holds.]

7. ∃　there exists  [mizar]  ex  (build in Mizar system)

 [usage]  1. ex a [There exists a.]

2. ex a st P [There exists a such that P holds.]

3. ex a being set st P [There exists a set a such that P holds.]

8.  T（1，t ，⊺ ，true, TRUE） truth  [mizar]  not contradiction (build in Mizar system)

[usage]  A & not contradiction  [A and TRUE]

TRUE  (margrel:def 14)

                           [usage]   TRUE = 1  [TRUE is equal to 1.]

9.       F （0，f ，⊥ ，falsum, FALSE）falsity, falsum  [mizar]  contradiction (build in Mizar system)

[usage]  A implies contradiction  [A implies FALSE]

 

FALSE  (margrel:def 13)

                           [usage]   FALSE = 0  [FALSE is equal to 0.]

 

 

＜The notations of set theory＞

 

1.      ∈　element (of set)  [mizar]  in (hidden:pred 1)

 [usage]  a in b  [a is an element of b: a belongs to b.]

2.      =  equality  (of set)  [mizar]  =  (hidden:pred 2) 

[usage]  a = b  [a is equal to b.]

3.      ≠　the negation of equality  (of set)  [mizar]  <>  (hidden:prednot 2)

[usage]  a <> b  [a is not equal to b.]

4.      { , }  finite set with elements  [mizar]  { , }  (tarski :def 1, etc.)

[usage]  {a}  [set with an element a.]; {a, b} [set with elements a, b], etc.

5.      ⊆　relation of inclusion (of set)  [mizar]  c=  (tarski:def 3)

[usage]  a c= b  [a is included in b: b includes a: a is a subset of b.]

6.      ∪　union (of set)  [mizar]  union  (tarski:def 3)

[usage]  union a   [the union of a]

7.  ∩  intersection (of set)  [mizar]  meet  (setfam_1:def 1)

[usage]  meet a   [the meet of a]

7.      [ , ]  ordered pair  [mizar]  [ , ]  (tarski:def 5)

[usage]  [a, b]   [the ordered pair of a and b]

8.   ∅   empty set  [mizar]  { }  (xbool_0:def 1)

[usage]  { }   [{ } has no element.]

9.  ∪  union (of two sets)  [mizar]  \/  (xbool_0:def 2)

              [usage]  a \/ b  [the union of a and b]

10. ∩  intersection (of two sets)  [mizar]  /\  (xbool_0:def 3)

[usage]  a /\ b  [the intersection of a and b]

11. ＼　difference (of two sets)   [mizar]  \  (xbool_0:def 4)

[usage]  a \ b  [the set { x : x is an element of a and x is not an element of b}]

12. ⊂　relation of proper subset( of set)  [mizar]  c<  (xbool_0:def 8)

[usage]  a c< b  [a is a proper subset of b]

13. ( ) c（ ￣ ）  complement (of set)   [mizar]  `  (subset_1:def 5)

[usage]  a `  [the complement of a]

14. ×　direct product of (sets)  [mizar]  [:,:]  (zfmisc_1:defs 3)

[usage]   [:a, b:]  [the direct product of a and b];

[:a, b, c:]  [the direct product of a, b and c], etc.

15.       P ( )  power set (of set)  [mizar]  bool  (zfmisc_1:def 1)

[usage]  bool a  [the power set of a]

16.       { x : P }  the set of elements x such that P holds )  [mizar]  { x : P }  (build in Mizar system)

[usage] 1. { x : P }  [the set of elements x such that P holds]

       2. { x where P : Q} [the set of element x satisfied with P such that Q holds]

 

 

＜The notations of the sets of numbers＞

 

1.       N  the set of natural numbers with 0  [mizar]  NAT (numbers:funcnod 1); omega  (ordinal2:def 5)

[usage]  0 in NAT  [0 is an element of N.]

2.       Z  the set of integers [mizar]  INT  (numbers:def 4)

[usage]  NAT c= INT  [N is a subset of Z.]

3.       Q  the set of rational numbers [mizar]  RAT  (numbers:def 3)

[usage]  NAT c= RAT  [N is a subset of Q.]

4.       R  the set of real numbers  [mizar]  REAL  (numbers:def 1)

[usage]  RAT c= REAL  [Q is a subset of R.]

5.       C  the set of complex numbers  [mizar]  COMPLEX  (numbers:def 2)

[usage]  REAL c= COMPLEX  [R is a subset of C.]

6.       On  the set of ordinals  [mizar]  On  (ordinal2:def 2)

[usage]  omega c= On  [ω is a subset of On.]

7.       ω　the least set of limit ordinals  [mizar]  omega  (ordinal2:def 5)

[usage]  0  in omega  [0 is an element of ω.]

 

 

＜The notations for functions (relations)＞

 

1.      dom  domain (of function (relation))  [mizar]  dom  (relat_1:def 4)

[usage]  dom f   [dom f  is the domain of  f.]

2.      im  (rng)  range (of function (relation))  [mizar]  rng  (relat_1:def 5)

[usage]  rng f   [rng f  is the range of  f.]

1.      ( )−1　inverse (of relation)  [mizar]  ~   (relat_1:def 7)

[usage]  r ~  [r ~ is the inverse relation of  r.]

2.      ( )−1　inverse (of function)  [mizar]  "   (relat_1:def 14)

[usage]  f "  [f "  is the inverse relation of  f.]

3.      ∘　composition (of function (relation))  [mizar]  *  (relat_1:def 8)

[usage]  f * g  [f * g  is the composition of f and g.]

6.  1/f  the reciprocal of function f  [mizar]  ^  (rfunct_1:def 8)

[usage]  f ^   [f ^ is the reciprocal of function f , that is, for every x, (f^)(x)=1/(f.x).]

7.  a・f  (af)  scalar product of a scalar a and a real function f  [mizar]  a (#) f (seq_1:def 5); a “ f (seq_1:def 5);

[usage]  (a (#) f) .b = a * (f.b)  [ (af)(b) = a(f(b) ) ];

               (a “ f) .b = a * (f.b)  [ (af)(b) = a(f(b) ) ]

1.       +  addition of functions  [mizar]   +  (seq_1:def 3)

[usage]  f + g  [f + g is addition of functions, that is , for every x, (f + g)(x) = f(x) +g(x).]

2.       −  subtraction of functions  [mizar]   -  (seq_1:def 4)

[usage]  f - g  [f - g is subtraction of functions, that is , for every x, (f - g)(x) = f(x) - g(x).]

3.       ・  multiplication of functions  [mizar]   (#)  (seq_1:def 1)

[usage]  f (#) g  [f (#) g  is product of functions, that is , for every x, (f (#) g )(x) = f(x)・g(x).]

4.        f/g  fraction of functions  [mizar]   /  (rfunct_1:def 4)

[usage]  f/g  [f/g is fraction of functions, that is , for every x, (f/g)(x)=(f(x)/g(x)).]

5.       −  the inverse of function with respect to addition  [mizar]   -  (seq_1:def 7)

[usage]  - f  [ -f  is inverse of function with respect to addition, that is , for every x, (-f )(x) = -f(x) .]

13.  |  restriction  (of function (relation))  [mizar]  |  (relat_1:def 11)

[usage]  f | a  [f | a  is the restriction of f with respect to a.]

14.  f (a)  image of a value a (with respect to function (relation) f )  [mizar]  f.a  (funct_1:def 4)

[usage]  f.a  [f.a  is the image of a with respect to f.]

15.   f (A)  image of set A of values (with respect to function (relation) f )   [mizar]  f .: A (relat_1:def 13)

[usage]  f.:A  [f.:A  is the image of set A of values with respect to f.]

16.  Hom(X, Y)  the set of functions with domain X and range Y  [mizar]  Funcs( , ) (funct_2:def 2)

[usage]  f in Funcs(X, Y) implies rng f = Y [(f is an element of Hom(X, Y)) implies rng f = Y.]

 

 

＜The notations of arithmetic＞

 

1.       +  addition  [mizar]  +  (xcmplx_0:def 4)

[usage]  a + b  [a + b is the sum of a and b.]

2.       ・ （×）  multiplication  [mizar]  *  (xcmplx_0:def 5)

[usage]  a * b  [a * b is the product of a and b.]

3.       −  subtraction  [mizar]  -  (xcmplx_0:def 8)

[usage]  a - b  [a - b is the difference of a and b.]

4.  −  negative sign (minus sign)  [mizar]  -  (xcmplx_0:def 6)

[usage]  - a  [-a is a negative number.]

5.      /  fraction  [mizar]  /  (xcmplx_0:def 9)

[usage]  a / b  [a / b is a fraction with numerator a and denominator b.]

6. 1/a  the reciprocal (number) of a   [mizar]  "  (xcmplx_0:def 7)

[usage]  a"  [a"  is the reciprocal (number) of a, that is 1/a.]

7. ÷  division  [mizar]  div  (int_1:def 7)

[usage]  a div b  [a div b is the quotient when b devides a.]

6.       mod  residue  [mizar]  mod  (int_1:def 8)

[usage]  a mod b  [a mod b is the remainder when b devides a.]

7.       |　devides  [mizar]  devides  (int_1:def 9)

[usage]  a | b  [a | b means that a devides b.]

8.       lcm  the least common multiple (of two natural numbers)  [mizar]  lcm (nat_1:def 4

[usage]  a lcm b  [a lcm b is the least common multiple of a and b.]

11. lcm  the least common multiple (of two integers)  [mizar]  lcm’  (int_2:def 2

[usage]  a lcm’ b  [a lcm b is the least common multiple of |a| and |b|.]

12.  gcd  the greatest common divisor of two natural numbers)  [mizar]  hcf (nat_1:def 5)

[usage]  a hcf b  [a gcd b is the greatest common divisorof a and b.]

13.  gcd  the greatest common divisor (of two integers)  [mizar]  gcd  (nat_1:def 5)

[usage]  a gcd b  [a gcd b is the greatest common divisor of |a| and |b|.]

14.   ‘  successor function  [mizar]  succ  (ordinal1:def 1)

[usage]  succ a   [succ a is the successor of a]

15. ≦ inequality with equality  [mizar]  <=  (xreal_0:def 2)

[usage]  1 <= 2   [1 is smaller than 2.]

16. ＞ inequality  [mizar]  >  (xreal_0: prednot 4)

[usage]  2 > 1   [2 is larger than 1.]

17. ≧  inequality with equality  [mizar]  =>  (xreal_0:prednot 2)

              [usage]  2 => 1   [2 is larger than 1.]

18. ＜ inequality  [mizar]  <  (xreal_0:prednot 2)

[usage]  1 < 2   [1 is smaller than 2.]

19.  min  minimum  [mizar]  min  (extreal2:def 1)

[usage]  min(2,3) = 2   [2 is minimum with respect to 2 and 3.]

20.  max  maximum  [mizar]  max  (extreal2:def 2)

[usage]  max(2,3) = 3   [3 is maximum with respect to 2 and 3.]

21.  !  factorial (of a natural number)  [mizar]  !  (sin_cos:def 30)

[usage]  a !  [a ! is the factorial of a natural number a]

20. [  ]　Gauss’ symbol  [mizar]  [\  /] (int_1:def 4)

[usage]  [\ a/]   [[\ a/] is [a].」

21. a ≡ b (mod c)  a and b are congruent modulo c [mizar] , are_congruent_mod  (int_1:def 3)

[usage]  a , b are_congruent_mod c [(a , b are_congruent_mod c) means (a ≡ b (mod c) )]

 

 

＜The notations of numbers and special constants＞

 

1.       0  numeral zero  [mizar]  0

2.       1  numeral one  [mizar]  1 ; one (ordinal2:def 2)

3.       2  numeral two  [mizar]  2

4.       3  numeral three  [mizar]  3

5.       4  numeral four  [mizar]  4

6.       5  numeral five  [mizar]  5

7.       6  numeral six  [mizar]  6

8.       7  numeral seven  [mizar]  7

9.       8  numeral eight  [mizar]  8

10.   9  numeral nine  [mizar]  9

11.   π circle ratio  [mizar]  PI  (sin_cos:def 30)

[usage]  3 < PI   [πis greater than 3.]

12.   e  Napier’s number  [mizar]  number_e  (power:def 4)

[usage]  2 < number_e   [e is greater than 2.]

13.   i  imaginary number  [mizar]  <i>  (xcmplx_0:def 1)

14.   ∞　infinity  [mizar]  +infty  (supinf_1:def 1) or  –infty  (supinf_1:def 3)

15.   +∞ infinity  [mizar]  +infty  (supinf_1:def 1)

16.   −∞　infinity  [mizar]  –infty  (supinf_1:def 3)

 

 

＜The notations for elementary functions and complex numbers＞

 

1.      sin  [mizar]  sin  (sin_cos:def 30)

[usage]  sin a   [the sine of a.]

2.      cos  [mizar]  cos  (sin_cos:def 22)

[usage]  cos a   [the cosine of a.]

3.      tan  [mizar]  tan  (sin_cos4:def 1)

[usage]  tan a   [the tangent of a.]

4.      sec  [mizar]  sec  (sin_cos4:def 4)

[usage]  sec a   [the second of a.]

5.      cot  [mizar]  cot  (sin_cos4:def 2)

[usage]  cot a   [the cotangent of a.]

6.      arcsin  [mizar]  arcsin  (sin_cos6:def 1)

[usage]  arcsin a   [the arcsine of a.]

7.      arccos  [mizar]  arccos  (sin_cos6:def 3)

[usage]  arccos   [the arccosine of a.]

8.      ex  exponential function (of real values)  [mizar]  exp  (sin_cos:def 26)

[usage]  exp x   [the exponential function of x]

9.      Re  the real part of a complex number  [mizar]  Re  (complex1:dfs 1)

[usage]  Re a   [the real part of a complex number a]

10.  Im  the imaginary part of a complex number  [mizar]  Im  (complex1:dfs 2)

[usage]  Im a   [the imaginary part of a complex number a]

11.  √　positive square root (of a real number)  [mizar]  sqrt  (square_1:def 4)

[usage]  sqrt a   [the square root of a]

12.   n√ positive n-powered root (of a real number)  [mizar]  n-Root  (prepower:def 3)

[usage]  3 -Root a  [the positive cubic root of a]

13.   ( ) 2  squre (of a number)  [mizar]  ^2  (square_1:def 3)

[usage]  a^2   [the square of a]

14.   ( ) 2  squre (of a number)  [mizar]  sqr  are_1:def 3)

[usage]  a^2   [the square of a]

15.  ab  a real number with exponent of a natural number [mizar]  |^  (newton:def 1)

[usage]  a |^ b  [the b times power of real number a]

16.  ab  a real number with exponent of an integer [mizar]  #Z  (prepower:def 4)

[usage]  a #Z b  [the b times power of real number a]

17.  ab  a real number with exponent of a rational namber [mizar]  #Q  (prepower:def 5)

[usage]  a #Q b  [the b power of real number a]

18.  ab  a real number with exponent of a real number [mizar]  #R  (prepower:def 8)

[usage]  a #R b  [the b power of real number a]

19.  ab  a real number with exponent of a real number [mizar]  to_power  (power:def 2)

[usage]  a to_power b  [the b power of real number a]

20. | | absolute value (of a complex number)  [mizar] abs (complex1:func 18)

[usage]  abs a  [the absolute value of a]

21.  ￣　conjugate complex number (of complex number) [mizar]  *’   (complex1:def 15)

              [usage]   <i>*’  [<i>*’ = −<i>]

22.  log  logarithm  [mizar]  log( , )  (power:def 3)

[usage]  log(a,b)  [log(a,b) is a logarithm with base of logarithm a and anti-logarithm b.]

23.  a + bi  a complex number with its real part a and its imaginary part b ), where a and b are real numbers  [mizar]  [*a,b*]  (arytm_0:def 7)

              [usage] for a being Element of REAL holds [*a,0*] in REAL  [It means that for a∈R，a+0i∈R holds.]

24.  arg  the argument of a complex number [mizar]  Arg  (comptrig:def 1)

[usage]  Arg a  [Arg a is the argument of a complex number a.]

 

 

＜The notations for limit and series＞

 

1.      lim  limit of complex sequence  [mizar]  lim  (comseq_2:def 5)

[usage]  1. lim a [the limit of complex sequence a]

2.  lim (a+b) = lim a + lim b  [This holds if a and b are convergent.]

2.      ∑　pertial sum of a real sequence  [mizar]  Percial_Sums  (series_1:def 1)

[usage]  Percial_Sums a  [pertial sum of real sequence a]

3.      ∑　sum of infinite series   [mizar]  Sum  (series_1:def 3)

[usage]  1. Sums a  [sum of infinite series of a real sequence a]

           2. Sums a = lim Percial_Sums a [The sum of infinite series of a real sequence a is equal to the limit of the pertial sum of it.]

4.      →+∞　(for a real sequence) divergent to the plus infinity  [mizar]  (is) divergent_to+infty  (limfunc1:def 4)

[usage]  a is divergent_to+infty  [The real sequence a is divergent to the plus infinity, that is , a →+∞.]

5.      →−∞　(for a real sequence) divergent to the minus infinity  [mizar]  (is) divergent_to-infty  (limfunc1:def 5)

[usage]  a is divergent_to-infty  [The real sequence a is divergent to the minus infinity, that is , a →−∞.]

6.

 limit b of a real function（x → a ） [mizar]　lim( , )  (limfunc3: def 4)

[usage]  lim(f ,a) = b  [f is convergent to b in a.]

7.

 limit b of a real function（x → a + 0 ） [mizar]　lim_right( , ) (limfunc2: def 8)

[usage]  lim_right(f ,a) = b  [f is right-convergent to b in a.]

8.

 limit b of a real function（x → a − 0 ） [mizar]　lim_left( , ) (limfunc2: def 7)

[usage]  lim_left(f ,a) = b  [f is left-convergent to b in a.]

9.

a real function f is divergent to +∞（x → a） [mizar] is_divergent_to+infty_in  (limfunc3: def 2)

[usage]  f is_divergent_to+infty_in a  [f is divergent to +∞ in a.]

10.

a real function f is divergent to −∞（x → a） [mizar] is_divergent_to-infty_in (limfunc3: def 3)

[usage]  f is_divergent_to-infty_in a  [f is divergent to −∞ in a.]

11.

 a real function f is divergent to +∞（x → a + 0 ） [mizar] is_right_divergent_to+infty_in  (limfunc2:def 5)

[usage]  f is_ right_divergent_to+infty_in a  [f is right-divergent to +∞ in a.]

12.

 a real function f is divergent to −∞（x → a + 0 ） [mizar] is_right_divergent_to-infty_in  (limfunc2:def 6)

[usage]  f is_ right_divergent_to-infty_in a  [f is right-divergent to −∞ in a.]

13.

 a real function f is divergent to +∞（x → a − 0 ） [mizar] is_left_divergent_to+infty_in  (limfunc2:def 2)

[usage]  f is_ left_divergent_to+infty_in a  [f is left-divergent to +∞ in a.]

14.

 a real function f is divergent to −∞（x → a − 0 ） [mizar] is_left_divergent_to-infty_in  (limfunc2:def 3)

[usage]  f is_ left_divergent_to-infty_in a  [f is left-divergent to −∞ in a.]

15.

 limit of a real function（x → +∞ ） [mizar]  lim_in+infty (limfunc1:def 12)

              [usage]  lim_in+infty f = a  [the limit a of a real function f in the plus infinity]

16.

 limit of a real function（x → −∞ ） [mizar]  lim_in-infty (limfunc1:def 13)

              [usage]  lim_in-infty f = a [the limit a of a real function f in the minus infinity]

17.

(for a real function) divergent to the plus infinity (x →+∞)  [mizar]  (is) divergent_in+infty_to-infty  (limfunc1:def 7)

[usage]  f is divergent_in+infty_to-infty  [The real function f is divergent to the plus infinity when x →+∞.]

18.

(for a real function) divergent to the minus infinity  (x →+∞)  [mizar]  (is) divergent_in+infty_to-infty  (limfunc1:def 8)

[usage]  f is divergent_in+infty_to-infty  [The real function f is divergent to the minus infinity when x →+∞.]

19.

 (for a real function) divergent to the plus infinity  (x →−∞)  [mizar]  (is) divergent_in-infty_to+infty  (limfunc1:def 10)

[usage]  f is divergent_in-infty_to+infty  [The real function f is divergent to the plus infinity when x →−∞.]

20.

(for a real function) divergent to the minus infinity  (x →−∞)  [mizar]  (is) divergent_in-infty_to-infty  (limfunc1:def 11)

[usage]  f is divergent_in-infty_to-infty  [The real function f is divergent to the minus infinity when x →−∞.]

 

 

＜The notations for differentiation and integral＞

 

1.      ( , )  open interval  [mizar]  ]. , .[  (rcomp_1:def 2)

[usage]  ].0 , 1.[  [This is the open interval between 0 and 1.]

2.      ] , [  open interval  [mizar]  ]. , .[  (rcomp_1:def 2)

[usage]  ].0 , 1.[  [This is the open interval between 0 and 1.]

3.  f’(a)  differential coefficient of real function f in a  [mizar] diff(f, a)  (fdiff_1:def 6)

[usage]  diff(f + g, a) = diff(f, a) + diff(g, a) [This means (f + g)’ (a) = f’ (a) +  g’(a) ]

4. f ‘ (x) (x∈a) the differential of a real function f differentiable on a ⊆ R  [mizar]  f `|a  (fdiff_1:def 8)

[usage]  f `|REAL  [This is the differential of the real function f differentiable on R.]

5. f ‘  the differential of a real function f differentiable on R  [mizar]  f `|REAL  (fdiff_1:def 8)

[usage]  (f `|REAL).a [This is the differential coefficient of the real function f in a .]

6.

　indefinite Riemann integral of a real function  [mizar]  integral  [integra1:def 18]

 

 

＜The notations for geometry＞

 

1.  AB  line through A and B in 3 dimentional Euclidian space [mizar]  Line( , )  (euclid_1:def 1)

[usage]  1. Line(A,B) st A, B in REAL 3  [line through A and B in 3 dimentional Euclidian space, where A, B are real 3-tuples.]

         2. for A, B st A, B in REAL 3 holds Line(A,B) = Line(B,A) [line through A and B is equal to line through B and A.]

 

＜The notations for probability＞

 

1.  Pr  probability  [mizar]  Probability (of )   (prob_1:def 13)

[usage]  Probability of X  [This means Pr(X), that is, the probability of an event X.]

 

 

＜The notations for vectors and matrices＞

 

1.      A is an n×m matrix over R  [mizar] A is Matrix of n,m,REAL  (matrix_1: def 3)

2.      A is an n×m matrix over C  [mizar] A is Matrix of n,m,COMPLEX  (matrix_1: def 3)

3.       

 1×… matrix a  (line vector)  [mizar]  <*a*>  (matrix_1:11)

4.

 1×ｎ matrix a  (line vector)  [mizar]  <*a*> st width <*a*> = n (matrix_1:11; matrix_1: def 4)

4.       

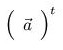…×1 matrix  a  (column vector)  [mizar]  <*a*>@  (matrix_1:11; matrix_1: def 7 )

5.       

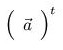n×1 matrix a  (column vector)  [mizar]  <*a*>@ st width <*a*> = n  (matrix_1:11; matrix_1: def 7 )

6.       

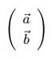 2×… matrix  [mizar]  <*a,b*>  (matrix_1:12)

7.       

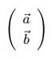 2×n  matrix  [mizar]  <*a,b*> st width <*a,b*> = n (matrix_1:12; matrix_1: def 4)

8.

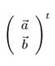…×2  matrix  [mizar]  <*a,b*>@  (matrix_1:12; matrix_1: def 7)

9.

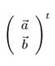ｎ×2  matrix  [mizar]  <*a,b*>@ st width <*a*> = n (matrix_1:12; matrix_1: def 7)

10.

 1×1 matrix with element a  matrix  [mizar]  <*<*a*>*>  (matrix_1:15)

11.

1×2 matrix with elements a and b  [mizar]  <*<*a*>,<*b*>*>  (matrix_1:15)

12.

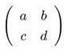2×2 matrix with elements a, b, c and d  [mizar]  <*<*a,b*>,<*c,d*>*>  (matrix_1:15)

13.

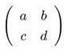2×2 matrix with elements a, b, c and d  [mizar]  (a,b)][(b,c)  (matrix_2:def 2)

14.

 (i, j)-element of a matrix a  [mizar]  A*(i,j)  (matrix_1:def 6)

15.  At  transposed matrix of A  [mizar]  @  (matrix_1:def 7)

[usage]  A@  [A@ is the transposed matrix of A.]

16.   +  addition of matrices   [mizar]  +   (matrix_1:def 7)

[usage] a + b [the sum of matrices a and b]

17.  −  minus sign of matrix  matrices   [mizar]  -   (matrix_1:def 13)

[usage]   -a   [the inverse of a matrix a with resprect to addition]

18.  ・ (×　or nothing)  multiplication of matrices   [mizar]  *  (matrix_3:def 4)

[usage] a * b [the product of matrices a and b]

19.   ( , ) ( < , > )  the inner product of finite sequences recognized as vectors  [mizar]  “*”  (fvsum_1:def 10)

[usage]   a“*”b   [the inner product of finite sequences a and b recognized as vectors]

20.   the n-th line of a matrix  a  [mizar]  Line(a,n)  (matrix_1:def 8)

21.   the n-th colum of a matrix  a  [mizar]  Col(a,n)  (matrix_1:def 9)

22.   O  n×m zero matrix  [mizar]  0.(n,m)  (matrix_1:def 11)

23.   E  (  I  )  n×n unit matrix  [mizar]  1.(n,m)  (matrix_1:def 12)

24.   det a  the determinant of a matrix a  [mizar]  Det  (matrix_1:def 12)

[usage]   Det a  [the determinant of a matrix a]