def 2 func X U Y -> set means x C it iff x C X or x C Y;
def 3 func X  Y -> set means x
Y -> set means x C it iff x C X & x C Y;
def 4 func X  Y -> set means x
Y -> set means x C it iff x C X & not x C Y;
def 5 pred X meets Y means ex x st x C X & not x C Y;
def 7 func X
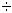 Y -> set means it = (X
Y -> set means it = (X  Y) U (Y
Y) U (Y  X);
X);def 8 pred X = Y means X c= Y & Y c= X;
8 x C X U Y iff x C X or x C Y;
9 x C X  Y iff x
Y iff x C X & x C Y;
10 x C X  Y iff x
Y iff x C X & not x C Y;
12 x C X & X misses Y implies not x C Y;
13 x C X & x C Y implies X meets Y;
15 X meets Y implies ex x st x C X & x C Y;
17 (for x st x C X holds not x C Y) implies X misses Y;
18 (for x holds x C X iff x C Y or x C Z) implies X = Y U Z;
19 (for x holds x C X iff x C Y & x C Z)implies X = Y  Z;
Z;
20 (for x holds x C X iff x C Y & not x C Z) implies X = Y  Z;
Z;
23 x C X 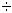 Y iff not (x
Y iff not (x C X iff x C Y);
24 x C X & x C Y implies X  Y < >
Y < >  ;
;
25 (for x holds not x C X iff (x C Y iff x C Z))implies X = Y 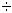 Z;
Z;
27  c= X;
c= X;
28 X c= Y & Y c= X implies X = Y;
29 X c= Y & Y c= Z implies X c= Z;
30 X c=  implies X =
implies X =  ;
;
31 X c= X U Y;
32 X c= Z & Y c= Z implies X U Y c= Z;
33 X c= Y implies X U Z c= Y U Z;
34 X c= Y & Z c= V implies X U Z c= Y U V;
35 X c= Y implies X U Y = Y;
37 X  Y c= X;
Y c= X;
38 X  Y c= X U Z;
Y c= X U Z;
39 Z c= X & Z c= Y implies Z c= X  Y;
Y;
40 X c= Y implies X  Z c= Y
Z c= Y  Z;
Z;
41 X c= Y & Z c= V implies X  Z c= Y
Z c= Y  V;
V;
42 X c= Y implies X  Y = X;
Y = X;
44 X c= Z implies X U Y  Z = (X U Y)
Z = (X U Y)  Z;
Z;
45 X  Y =
Y =  iff X c= Y;
iff X c= Y;
46 X c= Y implies X  Z c= Y
Z c= Y  Z;
Z;
47 X c= Y implies Z  Y c= Z
Y c= Z  X;
X;
48 X c= Y & Z c= V implies X  V c= Y
V c= Y  Z;
Z;
49 X  Y c= X;
Y c= X;
50 X c= Y  X implies X =
X implies X =  ;
;
51 X c= Y & X c= Z & Y  Z =
Z =  implies X =
implies X =  ;
;
52 X c= Y U Z implies X  Y c= Z & X
Y c= Z & X  Z c= Y;
Z c= Y;
53 (X  Y) U (X
Y) U (X  Z) = X implies X c= Y U Z;
Z) = X implies X c= Y U Z;
54 X c= Y implies Y = X U (Y  X);
X);
55 X c= Y & Y  Z =
Z =  implies X
implies X  Z =
Z =  ;
;
56 X = Y U Z iff Y c= X & Z c= X & for V st Y c= V & Z c= V holds X c= V;
57 X = Y  Z iff X c= Y & X c= Z & for V st V c= Y & V c= Z holds V c= X;
Z iff X c= Y & X c= Z & for V st V c= Y & V c= Z holds V c= X;
58 X  Y c= X
Y c= X 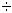 Y;
Y;
59 X U Y =  iff X =
iff X =  & Y =
& Y =  ;
;
60 X U  = X;
= X;
61 X 
 =
=  ;
;
62 X U X = X;
64 (X U Y) U Z = X U (Y U Z);
65 X  X = X;
X = X;
67 (X  Y)
Y)  Z = X
Z = X  (Y
(Y  Z);
Z);
68 X  (X U Y) = X;
(X U Y) = X;
69 X U (X  Y) = X;
Y) = X;
70 X  (Y U Z) = X
(Y U Z) = X  Y U X
Y U X  Z;
Z;
71 X U Y  Z = (X U Y) ∩ (X U Z);
Z = (X U Y) ∩ (X U Z);
72 (X  Y) U (Y
Y) U (Y  Z) U (Z
Z) U (Z  X) = (X U Y)
X) = (X U Y)  (Y U Z)
(Y U Z)  (Z U X);
(Z U X);
73 X  X =
X =  ;
;
74 X 
 = X;
= X;
75 
 X =
X =  ;
;
76 X  (X U Y) =
(X U Y) =  ;
;
77 X  X
X  Y = X
Y = X  Y;
Y;
78 (X  Y)
Y)  Y =
Y =  ;
;
79 X U (Y  X) = X U Y;
X) = X U Y;
80 X  Y U (X
Y U (X  Y) = X;
Y) = X;
81 X  (Y
(Y  Z) = (X
Z) = (X  Y) U X
Y) U X  Z;
Z;
82 X  (X
(X  Y) = X
Y) = X  Y;
Y;
83 (X U Y)  Y = X
Y = X  Y;
Y;
84 X  Y =
Y =  iff X
iff X  Y = X;
Y = X;
85 X  (Y U Z) = (X
(Y U Z) = (X  Y)
Y)  (X
(X  Z);
Z);
86 X  (Y
(Y  Z) = (X
Z) = (X  Y) U (X
Y) U (X  Z);
Z);
87 (X U Y)  (X
(X  Y) = (X
Y) = (X  Y) U (Y
Y) U (Y  X);
X);
88 (X  Y)
Y)  Z = X
Z = X  (Y U Z);
(Y U Z);
89 (X U Y)  Z = (X
Z = (X  Z) U (Y
Z) U (Y  Z);
Z);
90 X  Y = Y
Y = Y  X implies X = Y;
X implies X = Y;
91 X 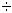 Y = (X
Y = (X  Y) U (Y
Y) U (Y  X);
X);
92 X 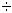
 = X &
= X & 
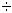 X = X;
X = X;
93 X 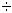 X =
X =  ;
;
95 X U Y = (X 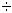 Y) U X
Y) U X  Y;
Y;
96 X 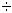 Y = (X U Y)
Y = (X U Y)  X
X  Y;
Y;
97 (X 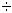 Y)
Y)  Z = (X
Z = (X  (Y U Z)) U (Y
(Y U Z)) U (Y  (X U Z));
(X U Z));
98 X  (Y
(Y 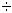 Z) = X
Z) = X  (Y U Z) U X
(Y U Z) U X  Y
Y  X;
X;
99 (X 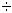 Y)
Y) 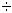 Z = X
Z = X 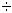 (Y
(Y 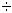 Z);
Z);
100 X meets Y U Z iff X meets Y or X meets Z;
101 X meets Y & Y c= Z implies X meets Z;
102 X meets Y  Z implies X meets Y;
Z implies X meets Y;
104 X misses  ;
;
110 X meets X iff X < >  ;
;
111 X  Y misses X
Y misses X  Y;
Y;
112 X  Y misses X
Y misses X 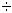 Y;
Y;
113 X meets Y  Z implies X meets Y;
Z implies X meets Y;
114 X c= Y & X c= Z & Y misses Z implies X =  ;
;
115 X  Y c= Z & Y
Y c= Z & Y  X c= Z implies X
X c= Z implies X 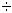 Y c= Z;
Y c= Z;
116 X  (Y
(Y  Z) = (X
Z) = (X  Y)
Y)  Z;
Z;
117 X  (Y
(Y  Z) = X
Z) = X  Y
Y  X
X  Z;
Z;
118 X misses Y iff X  Y =
Y =  ;
;
119 X meets Y iff X  Y < >
Y < >  ;
;
120 X c= (Y U Z) & X  Z =
Z =  implies X c= Y;
implies X c= Y;
121 Y c= X & X  Y =
Y =  implies Y =
implies Y =  ;
;