6.4 Functor Definition

We will explain the fuctor definition next. For example, let us think about a 2 variable fuctor. Let us assume that we want to make a new set Z from the set (set)X,Y. We will explain what to do at this point.



      X  Y -> Z
 


      set set   set



  definition



   let  X , Y  be set;



   func X  Y -> set



   means



   :N: x C it iff



      x C X & x C Y;



   existence ......;



   uniqueness



   proof



   end;



  end;

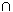This case also allows for it to be written in the operation form instead of the definition of a function like f (X,Y) =Z. Let us assume that we want to define such a symbol as Z=X Y. To make a new set Z from sets X and Y is truly this factor. With let X,Y be set;, if we have sets X, Y ready and this is also reserved, be set is not needed. In addition, func X 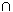Y -> set indicates X 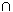Y as a set. The next line after means is the meaning of that factor. We will then write the meaning of the factor by placing a label like before. In this meaning, X 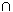Y is indicated as it.

In addition, in the demonstration section (contents of the meaning) , we have to demonstrate the existence and uniqueness. In other words, we have to express its existence and uniqueness.

For the demonstration for uniqueness, we only have to state the following.

If we take A1 and A2 as it:

x C A1 <=> x C X & x C Y

x C A2 <=> x C X & x C Y

A1 = A2

If we write this, it will be as below:



      uniqueness



       proof



        let A1,A2 be set such that



          A1: x C A1  iff  x C X  &  x C Y



          and



          A2: x C A2  iff  x C X  &  x C Y;



          now let y;



           y C A1 iff y C X  &  y C Y  by A1;



           hence y C A1  iff  y C A2  by A2;



          end;



         hence A1=A2 by TARSKI:2;

In short, when we bring in the two sets A1 and A2 that satisfy this condition, by demonstrating the equality of these two sets, the uniqueness is in fact demonstrated.

In this demonstration of uniqueness, because it is such that in the third line, one can see that after it the two sentences label A1 and label A2 are connected with and. It is stated as now let y. Let us assume that this y is reserved as Any. In addition, by label A1 we can state as y C A1 iff y C X & yC Y, and therefore, by label A2, yCA1 iff yCA2 can be stated. In addition, it means that enough necessary conditions for A1=A2 are demonstrated by TARSKI:2 stating that yCA1 and yCA2 are equally corresponding with the optional y; therefore, A1=A2 are demonstrated.

We also have to demonstrate the existence in the same way; however, we have to state that such an it exists.